[백준] 15661번 : 링크와 스타트 - JAVA [자바]

https://www.acmicpc.net/problem/15661

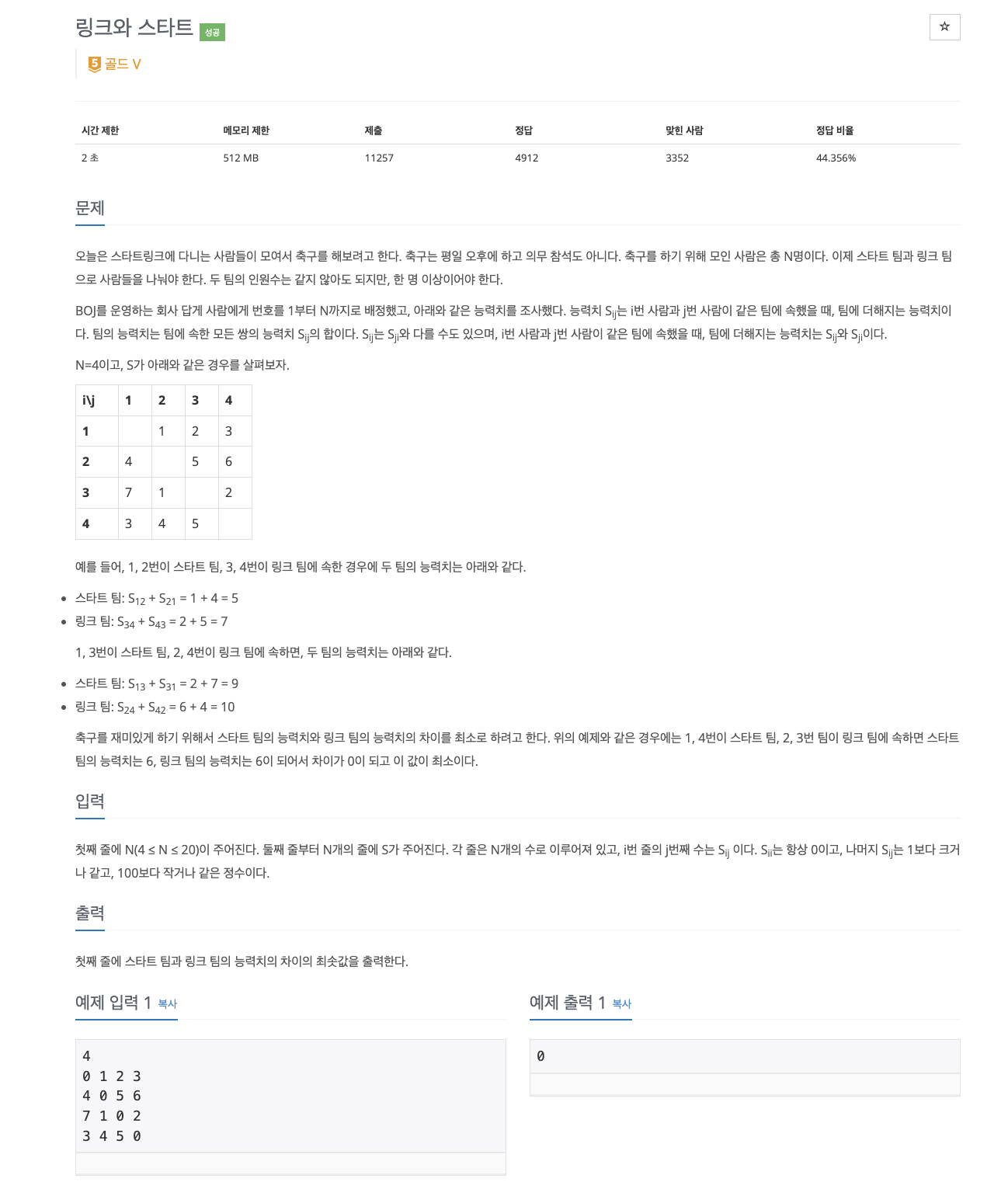
15661번: 링크와 스타트

---

문제

 

이 문제는 실버1 스타트와 링크의 후속 문제이다. 아래의 글을 먼저 보고오면 편하다.

https://bean-conding.tistory.com/10

[백준] 14889번 : 스타트와 링크 - JAVA [자바]

 

전 문제랑 차이가 있다면 팀의 멤버수가 같지 않아도 된다는 점이다.

그래서 나는 조합으로 풀지 않고, 부분 집합을 사용하여 풀었다.

 

아래와 같은 시나리오로 코드를 작성했다.

 

1. 팀을 나눌 부분집합을 구한다.

2. 로직을 돌리기전에 집합의 수가 전체 집합 크기와 같지않고, 1이상이어야 로직을 실행하게한다.

3. 두 팀의 점수차이를 구하는 calculation 메소드를 만들고 이를 통해 최소값을 저장한다. 

 

이게 끝이다.

 

아래는 기본 부분집합 코드이다.

static void subSet(int count) {
		
	if(count == N) {
		System.out.println(Arrays.toString(visit));
		return;
	}
		
		
	visit[count] = true;
	subSet(count + 1);
	visit[count] = false;
	subSet(count + 1);
}

 

 

위 사진과 같이 부분집합이 잘나오는 것을 확인할 수 있다.

 

이제 2번 로직인 크기검사를 해야됨으로, 나는 인자에 subSetCnt라는 변수를 추가해주었고, 재귀를 하면서 크기를 구하도록 변경해주었다.

 

아래는 변경된 부분집합 코드다.

static void subSet(int count, int subSetCnt) {
		
	if(count == N) {
		if(subSetCnt >= 1 && subSetCnt < N) {
			//여기서 두팀의 차이를 계산하는 로직 들어감.
		}
		return;
	}
		
		
	visit[count] = true;
	subSet(count + 1, subSetCnt + 1);
	visit[count] = false;
	subSet(count + 1, subSetCnt);
}

 

 

이제 이전 스타트와 링크에 있는 계산 메소드를 적용해주면 통과!

 

---

전체 코드

public class Main {
	static int N, result;
	static boolean[] visit;
	static int[][] map;

	public static void main(String[] args) throws Exception {
    	System.setIn(new FileInputStream("input.txt"));
    	BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    	StringBuilder sb = new StringBuilder();
    	StringTokenizer st;
    	
    	N = Integer.parseInt(in.readLine());
    	visit = new boolean[N];
    	map = new int[N][N];
    	result = Integer.MAX_VALUE;
    	
    	for(int i = 0; i < N; i++) {
    		st = new StringTokenizer(in.readLine());
    		
    		for(int j = 0; j < N; j++) {
    			map[i][j] = Integer.parseInt(st.nextToken());
    		}
    	}
    	
    	subSet(0, 0);
    	
    	System.out.println(result);
    }
	
	static void subSet(int count, int subSetCnt) {
		
		if(count == N) {
			if(subSetCnt >= 1 && subSetCnt < N) {
				calculation();
			}
			return;
		}
		
		
		visit[count] = true;
		subSet(count + 1, subSetCnt + 1);
		visit[count] = false;
		subSet(count + 1, subSetCnt);
	}
	
	static void calculation() {
		int startTeam = 0;
		int linkTeam = 0;
		
		for(int i = 0; i < N; i++) {
			
			for(int j = i + 1; j < N; j++) {
				
				if(visit[i] && visit[j]) {
					startTeam += map[i][j] + map[j][i];
				}
				else if(!visit[i] && !visit[j]) {
					linkTeam += map[i][j] + map[j][i];
				}
			}
		}
		
		result = Math.min(result, Math.abs(startTeam - linkTeam));
	}
}

 

 

---

결과

---

후기

비트마스킹을 이용한 부분집합을 구한다면 재귀가 아니라서 더욱 빠를 것이라 생각한다.

N = 4 일 경우 

0000 0001 .... 1110 1111 이렇게 비트마스킹으로 부분집합을 쉽게 구할 수 있다.

 

 

위 그림을 보면 의미있는 속도 차이가 나는 것을 볼 수있다.

 

부분집합을 구할 때 비트마스킹으로 먼저 생각해보는 습관을 들여야겠다!