https://www.acmicpc.net/problem/14225
14225번: 부분수열의 합
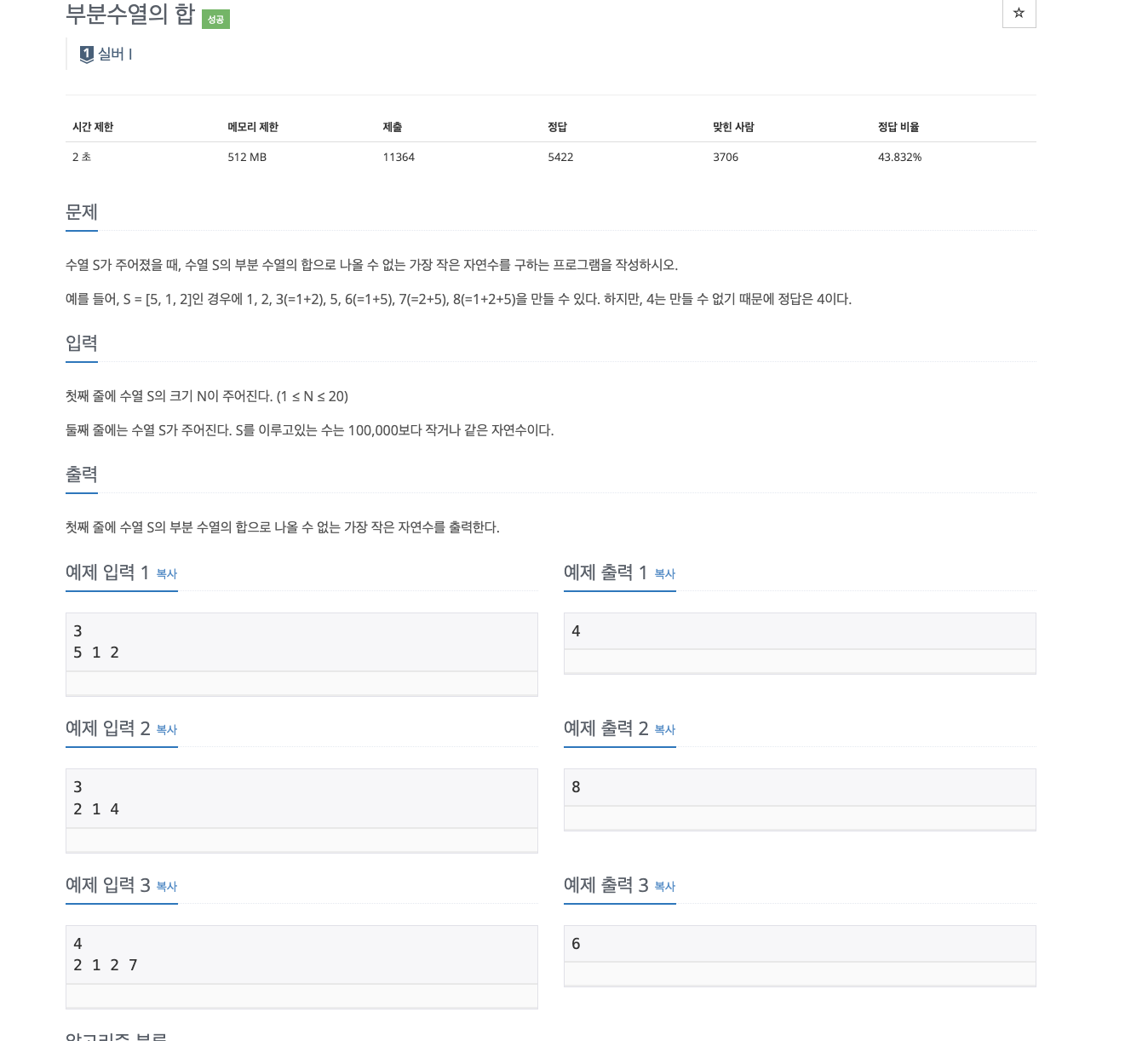
수열 S가 주어졌을 때, 수열 S의 부분 수열의 합으로 나올 수 없는 가장 작은 자연수를 구하는 프로그램을 작성하시오. 예를 들어, S = [5, 1, 2]인 경우에 1, 2, 3(=1+2), 5, 6(=1+5), 7(=2+5), 8(=1+2+5)을 만들
www.acmicpc.net
문제

아래 문제를 풀면서 부분집합을 비트마스킹으로 더 풀고 싶었고 부분집합 문제를 풀기위해 이 문제를 풀었다.
https://bean-conding.tistory.com/12
[백준] 15661번 : 링크와 스타트 - JAVA [자바]
https://www.acmicpc.net/problem/15661 15661번: 링크와 스타트 첫째 줄에 N(4 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에 S가 주어진다. 각 줄은 N개의 수로 이루어져 있고, i번 줄의 j번째 수는 Sij 이다. Si
bean-conding.tistory.com
내가 생각한 로직은
1. 부분집합을 구한다.
2. 부분집합들의 합을 구하고 리스트에 저장한다.
3. 저장된 리스트를 오름차순 정렬한다.
4. 결과값을 0으로 셋팅하고 +1 값이 리스트의 0인덱스부터 같은지 안같은지 검사한다.
- 만약 +1 한 값이 리스트의 인덱스 값과 일치하다면 결과값을 +1 해준다.
- 만약 결과값과 리스트의 인덱스 값과 일치하지 않다면 for 문을 중지한다.
아래는 비트마스킹을 이용한 부분집합 구하는 메서드이다.
// 비트마스킹으로 부분집합 구하는 메서드
static void bitSubSet() {
for(int i = 0; i < 1 << N; i++) {
int sum = 0;
for(int j = 0; j < N; j++) {
if((1 & i >> j) == 0) continue;
System.out.print(j + " ");
}
System.out.println();
}
}

위 코드를 실행하면 위 사진과 같이 부분집합이 구해지는 것을 알 수 있다.
1번 로직은 끝나고 이제 2,3,4번 로직은 단순 구현 해주면 끝이다.
어떻게 비트마스킹으로 부분집합을 구현할 수 있는지는 다음 블로그가 잘 설명해준다.
https://selina-park.tistory.com/103
[알고리즘_개념] 비트마스크 연산, 부분집합의 표현
부분집합이란? 예를 들어, 집합 A = {a, b, c, d}가 있다고 하면, A의 부분집합인 B는 {}, {a}, {b}, ... {a,b}, ... {a, b, c}, ... {a,b,c,d}, 16(2^4)가지수로 표현될 수 있다. 비트마스크 연산을 이용한 부분집합의
selina-park.tistory.com
전체 코드
public class Main {
static int N;
static String S;
static int[] arr;
static List<Integer> list;
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("input.txt"));
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
N = Integer.parseInt(in.readLine());
S = in.readLine();
st = new StringTokenizer(S);
arr = new int[N];
list = new ArrayList<>();
for(int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
bitSubSet();
// 3. 리스트를 오름차순 정렬후.
Collections.sort(list);
int result = 0;
// 4번 로직.
for(int i = 0; i < list.size(); i++) {
int num = list.get(i);
if(result + 1 == num) {
result++;
}
else if(result != num) {
break;
}
}
System.out.println(result + 1);
}
// 비트마스킹으로 부분집합 구하는 메서드.
static void bitSubSet() {
for(int i = 0; i < 1 << N; i++) {
int sum = 0;
for(int j = 0; j < N; j++) {
if((1 & i >> j) == 0) continue;
// 2번 로직 부분집합의 합을 구한다.
sum += arr[j];
}
if(sum == 0) continue;
// 합을 리스트에 저장.
list.add(sum);
}
}
}
결과

'Algorism > 백준' 카테고리의 다른 글
| [백준] 11048번 : 이동하기- JAVA [자바] (1) | 2024.01.03 |
|---|---|
| [백준] 5014번 : 스타트링크 - JAVA [자바] (1) | 2024.01.02 |
| [백준] 15661번 : 링크와 스타트 - JAVA [자바] (0) | 2024.01.02 |
| [백준] 2529번 : 부등호 - JAVA [자바] (0) | 2024.01.01 |
| [백준] 14889번 : 스타트와 링크 - JAVA [자바] (1) | 2024.01.01 |