Binary Tree 란?
- 모든 노드가 정확하게 두개의 서브트리를 가지고 있습니다.
- 서브트리는 공백이 될 수 있습니다.
- 노드의 유한 집합으로서 공백이거나 루트와 두 개의 분리된 이진트리인 경우 왼쪽 서브트리와 오른쪽 서브트리로 구성
- root가 0이 아닌 1에서 시작할 때, i 번째 노드에 대해서 parent(i) = i/2 , left_child(i) = 2i , right_child(i) = 2i + 1 의 index 값을 갖습니다.

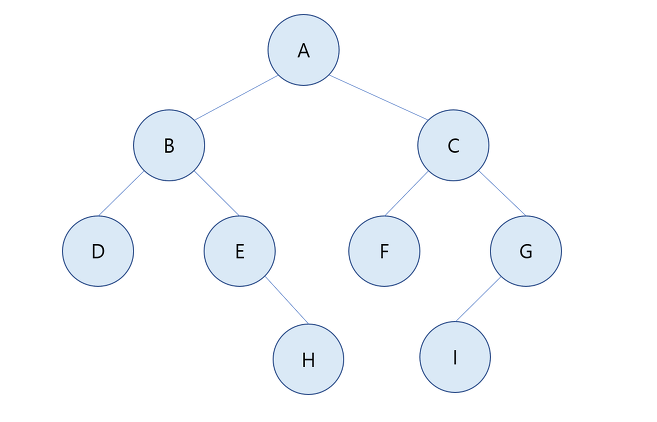
위의 그림을 보겠습니다!
두개의 서브 트리가 모두 공백인 리프 노드 - D, H, F, I
공백이 아닌 서브 트리를 하나씩 가지고있는 노드 - E, G
노드 E는 공백 왼쪽 서브트리와 오른쪽 서브트리 H를 가지고 있으며 노드 G는 왼쪽 서브트리I와 오른쪽 공백 서브트리를 가지고 있습니다!
제가 위에서 왼쪽 서브트리와 오른쪽 서브트리를 확실하게 구분한다고 하였는데 아래의 그림을 한번 보도록 하겠습니다!

일반 적으로의 트리에서는 위 두개의 트리는 같지만 이진 트리에서는 두개의 트리는 다른 트리입니다!
왜냐하면 이진트리에서는 서브트리의 위치가 다르기 때문입니다!
이진 트리의 종류
편향 이진트리(Skewed binary tree)
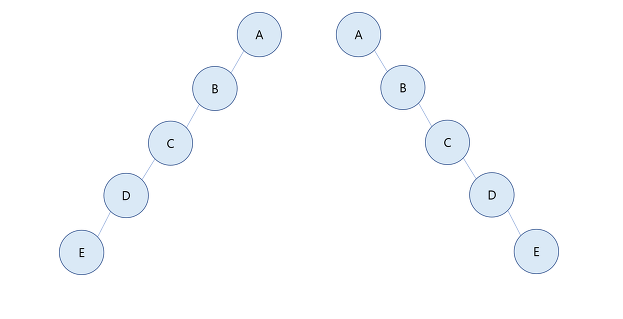
윗 그림을 보시면 편향 이진트리를 보여주고 있습니다!
편향 이진트리란 모든 노드가 부모의 왼쪽 자식이기 때문에 왼편으로 편향되어 있거나 반대로 모든 노드가 부모의 오른쪽 자식으로 되어 오른쪽으로 편향되어 있어야 합니다!
포화 이진트리(full binary tree)

포화 이진트리란 이진트리가 보유할 수 있는 최대의 노드를 가지고 있는 형태입니다. 높이하 h인 이진 트리에서 있을 수 있는 최대 노드 수는
2h+1-1입니다. 아래 그림은 높이가 2인 포화 이진트리이므로 최대 노드수는 7개입니다!
완전 이진트리(complete binary tree)
만일 높이가 h이고 노드 수가 n 일때 n <= (2h+1-1)인 이진트리를 노드의 레벨 순수에 따라 노드 번호를 붙인다면 이때 각 노드 번호의 위치가 포화 이진트리 번호 1에서 n까지의 위치와 모두 정확하게 일치한다면 이 트리를 완전 이진트리라고 합니다!
쉽게 설명하자면 루트 노드를 1이라고 하고 그외에 모든 노드가 왼쪽에서 오른쪽까지 꽉차서 n 일때 n <= (2h+1-1)라면 완전 이진트리입니다.

'CS > DataStructure' 카테고리의 다른 글
| 이진 탐색 트리 (Binary Search Tree) (0) | 2022.09.05 |
|---|---|
| 트리(Tree)란? (0) | 2022.08.30 |
| Stack and Queue (0) | 2022.08.16 |
| Array vs Linked List (0) | 2022.08.15 |