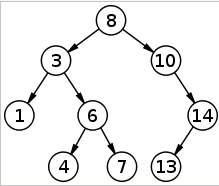
이진 탐색 트리 (Binary Search Tree)

이진 탐색 트리(Binary Search Tree)란?

---

•  각 노드에 중복되지 않는 키(Key)가 있다.
• 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
• 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
• 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.

 

이진 탐색 트리의 예시

이진 탐색 트리의 특징

---

이진 탐색 트리는 기존 이진트리보다 탐색이 빠릅니다.

이진 탐색 트리의 탐색 연산은 트리의 높이(height)가 h라면 O(h)의 시간 복잡도를 가집니다.

 

이진 탐색 트리의 탐색 과정을 한번 보시죠!

 

1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료합니다.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행합니다.
3. 찾고자 하는 값이 루트노드의 키보다 크다면 오른쪽 서브트리로 탐색을 진행한다.
4. 위 과정 반복!

이진 탐색 트리의 탐색 예시

 

이진 탐색 트리 삽입

---

1.  삽입할 값을 루트 노드와 비교해 같다면 오류를 발생합니다 -> 이진 탐색의 특징에 위반 됩니다!
2. 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색하여 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교합니다.
3. 삽입할 값이 루트노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교합니다.

 

2를 키로 가진 노드를 삽입하는 예시를 보도록 하겠습니다!

 

이진 탐색 트리의 삽입과정 예시

 

이진 탐색 트리의 삭제

---

이진 탐색 트리의 삭제는 조금 복잡합니다.. 이진 탐색 트리에서 특정 노드를 삭제할 때 아래와 같은 3가지 상황을 나누어 구현해야됩니다!

 

1. 삭제하려는 노드가 단말 노드일 경우
2. 삭제하려는 노드의 서브 트리가 하나인 경우
3. 삭제하려는 노드의 서브 트리가 두 개인 경우

 

삭제하려는 노드가 단말 노드일 경우

단말 노드의 삭제는 간단합니다. 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 Null로 만들고, 삭제할 노드를 삭제 해주면 됩니다.

 

단말 노드의 삭제 예시

 

삭제 할려는 노드의 서브 트리가 하나인 경우

삭제할 노드의 자식 노드를 삭제할 노드의 부모노드가 가르키게 하고 해당 노드를 삭제합니다!

서브 트리가 하나인 경우 삭제 예시

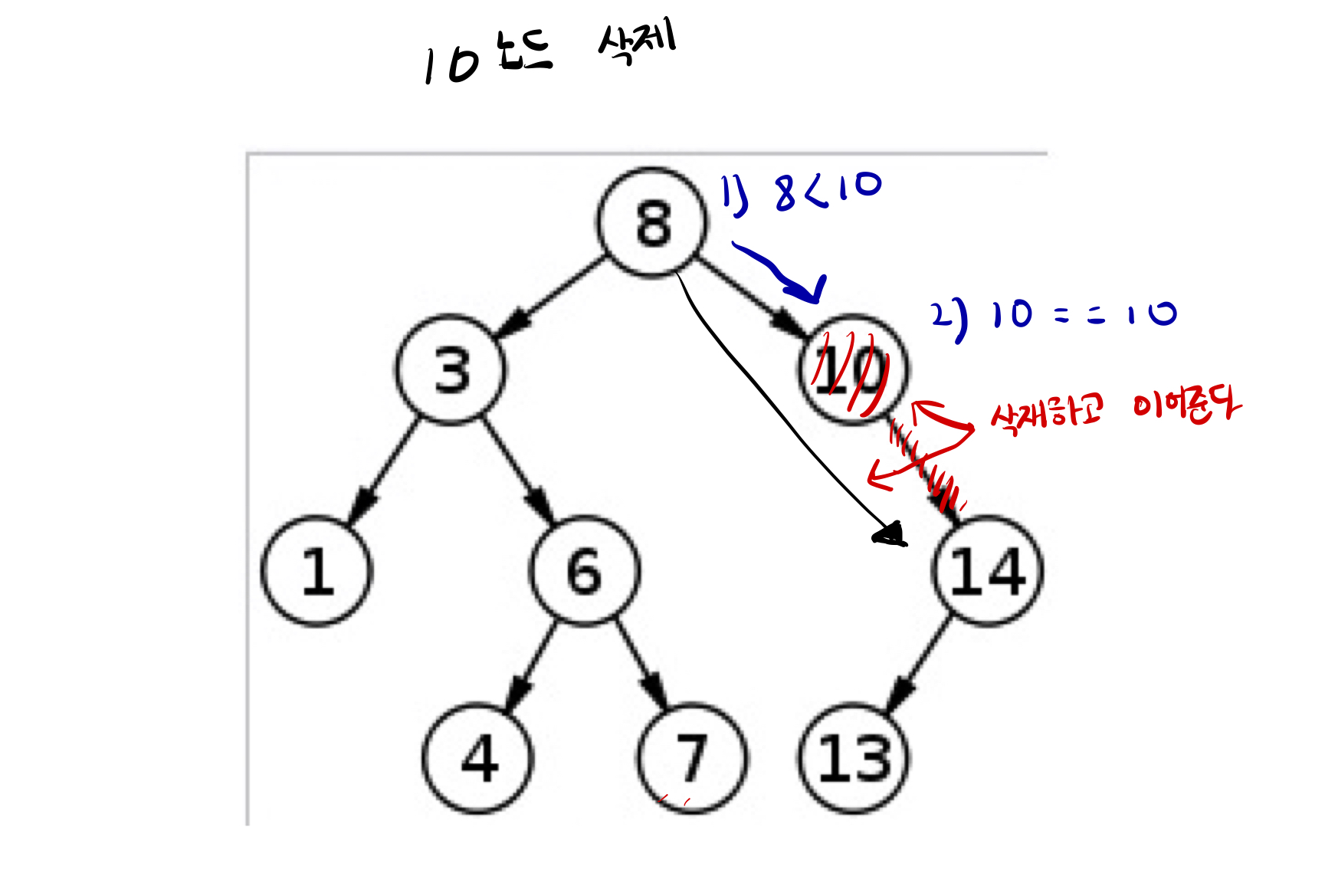
삭제하려는 노드의 서브트리가 두 개인 경우

이 경우 가장 복잡합니다! 이 경우 두 가지 방법을 사용할 수 있습니다.

 

1. 삭제할 노드 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리에 올린다.

 

(1) 번 방법의 삭제

 

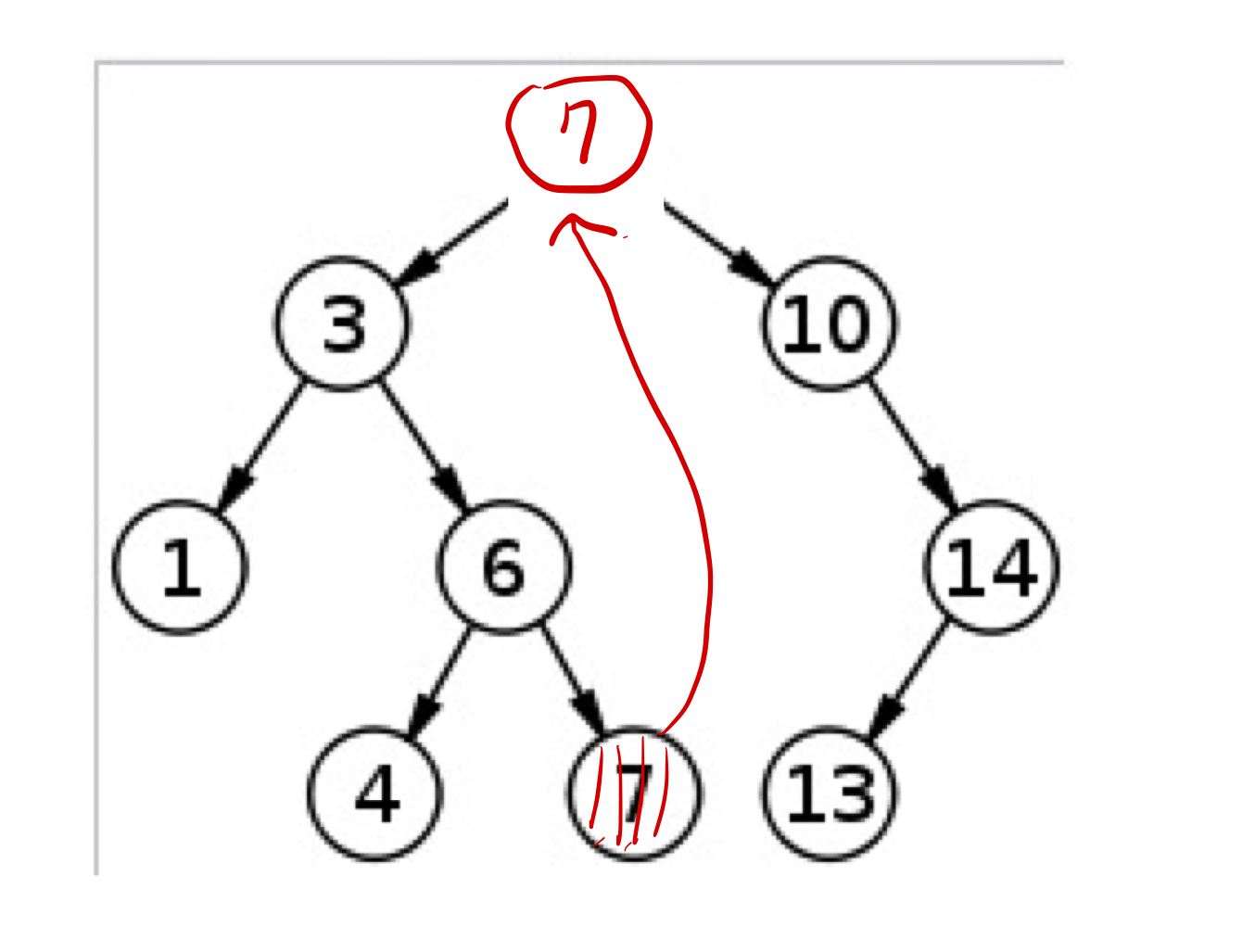
2. 삭제할 노드 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올린다.

(2) 번 방법의 삭제 예시